4.2te Seite: Die "Hubble-Konstante" und das ewig Maya Zyklisch Universum
Wir erstellen SCAq0113
te für diese Seite. Um unseren eigenen hohen Qualitätsansprüchen gerecht zu werden benötigen wir hierfür noch etwas Zeit.
SCAN0o36.JPEG
Bitte 22besuchen Sie diese Seite bald wieder. Vielen Dank für ihr Interesse!
EigSKARsEigScansR0017409
öööööööööööööööööööööööööööööööööööööööööööööööööööööööööööö
Neustart! Hier neuer Einstieg, wenn vom 1a-SonderSeite ankommend.
===================================================
Es geht im nachstehenden pdf-File-Text [um die Einbeziehung des Wissens bezüglich der Entwicklung der "Strukturierungen" des ZEITENRAUMES bzw. mit anderen Worten, es geht um eine Übersicht über die vermutlich-zeitliche Entwicklung des Universums.]
Am12tenMai2021revidiert Stand 17Mai2021
.
Gegenüberstellung der Unterschiede bzw. der Übereinstimmungen der beiden, {Urknall und Urprall} Klassik-Modellen,
zu dem bisher von dem 'Mainstream' einzig-zugelassenen Λ-CDM-Modell.
.
In allen Modellen gelten meine neuen Erkenntnisse [zu der logistischen Einordnung der ϿInflationsϾ-Phase] während des zweiteiligen Prozesses, das heißt,
_ während der ϾInflationsϿ-Phase oder
_ während der ϿExpansionsϾ-Phase
des Werdungs-Prozesses des Universums.
.
VorabFestlegungen von "Symbolik"Zeichen der »Entropie«:
===========================================
_‘Sterben‘ bedeutet ϿZerfallϾ, d.h. ϿEntropieϾ-Vergrößerung, z.B. beim Kaputtgehen der Tasse oder bei der ϿExpansionϾ; und deswegen, zeigen die ‘Anführungszeichen‘ beim ϿZerfallϾ an, dass sie [nach-außen-hin als „geöffnet“ verstanden] werden sollen.
_‘Leben‘ bedeutet ϾEmbryoϾ, d.h. ϾSymtropieϿ-Vergrößerung
bei ‘Strahlung‘ zu ‘Materie‘= auf /\ ab beim ϾInflationsϿ-Peak; deswegen wird sozusagen das ϾEmbryoϿ [nach innen hin mittels der ‘Anführungs-zeichen‘ „hermetisch eingeschlossen“].
Merke: (Wiederholung);
Während der ϿExpansionsϾ-Phase wird die ϿEntropieϾ größer. Zur symbolischen Kennzeichnung dieser ϿExpansionsϾ-Kinetik sollen deswegen die sogen. ‘Anführungzeichen‘ nach außen hin „geöffnet“ verstanden werden; das heißt, sich beim Leser so einprägen.
Dennoch ist schon während dieser nach „außen geöffneten“ ϿExpansionsϾ-Phase lokal die Verklumpung von Materie d.h. eine informelle ϾSelbstorganisationϿ erlaubt, so_dass es ‘lokal‘ zur ϾSymtropieϿ-Vergrößerung bis hin zur ϾEmbryonenϿ-Entstehung kommen kann und auch „naturgemäß- systematisch“ dazu kommen soll.
Verschiedene Modelle:
Es gibt die beiden KlassikModell-Typen:
„Urknall-Typ“ und „Urprall-Typ“ (mit teilweiser Übereinstimmung untereinander) einerseits und das prinzipiell dazu verschiedene
Λ-CDM-Modell andererseits:
.
Schilderung der Unterschiede bzw. Übereinstimmungen.
========================================
In (weiter unten befindlichen) ‘cten-Schaubild‘ namens
"Die natur-gesetzliche KosmoEntfernungsLeiter"
würden die Verläufe der gemessen «HubbleParameter»-Kurve zunächst erwartungsgemäß der sättigungsbegrenzten violetten Kurve folgen, wobei interessanterweise die Nobelpreis-MessPunkte der SNIae ganz in der Nähe des RAUMZEIT-KoordinatenBereichs für ‘hier&heute‘ also um "ž=1,0" herum zu liegen kämen.
Dort weist eine geschweifte Klammer auf „Die Kurve der Nobelpreis-Messungen“ hin.
Hinweis: Im ‘cten-Schaubild‘ hatte ich vorher den –(zum «Hubble-Dia-gramm» spiegelverkehrten Verlauf des Nobelpreis-»Hubble_plots«)– als MessKurve gehabt, wie man an der spiegelverkehrten Beschriftung noch erkennen kann. Die ungespiegelte ursprüngliche Grafik stammte noch von TuomoSuntola.
Mit der versuchten Extrapolation hatte ich beabsichtigt, bis auf "ž=10^–6" bzw. "D=10^–6[Mpc] =1[pc]" herab zu extrapolieren. Dabei habe ich allerdings gefunden, dass für "ž=10^–6" ein unerwartetes "D=10[pc]" anstatt des "D=1[pc]" herausgekommen ist. => Letzteres "D=1[pc]" sollte ja normgerecht für "D=150[Mio km]" passen.
Zur Erinnerung: Der Abstand (D=distance) von der Größe "1[AU=1[Astronomische Einheit]" also zirka "D=150 [Mio km]" für "D=1[pc]" würde für die Größe des Sonnen-Systems stehen.
Und, wir ‘Beobachter auf der Erde‘ müssten im Bereich "ž=10^(–7–6)= 10^–13" positioniert sein, um mit der Norm-Größe "D=1,50 [m]" eines irdischen Beobachters in beiden Klassik-Modellen als normgerechte ‘BasisRelation‘ gelten zu können.
Dazu der belehrende Hinweis: Gemäß der [1.]Zeile der Tab.[321]S342bis-S345 im ‘atenSchaubild‘ müsste ja im Kosmologischen Standard-Modell das heißt im Λ-CDM-Modell Abstand, "D=NULL[m]" als normgerechte ‘BasisRelation‘ gelten, (was ja physikalisch-mathematisch ‘völliger Unsinn‘ wäre).
Diese Tabelle vom ‘atenSchaubild‘ stammt aus dem Springer-Buch "Kleines 1x1 der Relativitätstheorie" von ElviraKrusch-&GottfriedBeyvers; und das Buch hat meine Lit.Nr. [321].
Die nachstehende Tabelle enthält insbesondere in der [3.]Zeile jene "(FranzEmbacher’sche) Rotverschiebungs-Entfernungs-Relation", welche für die Kinetik des mitbewegten Beobachters zutreffen soll.
In vorstehender Tabelle wird –(wie es auch für die Nobelpreis-Begründung ausgeführt wird,)– in der [6.]Spalte eine maximale Entfernung "5,8[MrdLJ]" genannt, wo sich das Λ-CDM -Universum von vorher „Abbremsung“ auf nunmehr andauernde „Beschleunigung“ umgestellt haben soll.
Und als Grund für die Umstellung von „begrenzter Abbremsung“ auf „ewige Beschleunigung“ wird ja als Spekulation bekanntlich bei der NobelpreisWürdigung ein [lediglich logisch begründbares] ‘Überwiegen‘ der sogen. "Dunklen_Energie" angegeben. Und, in allen Verlautbarungen seit 2011 wird nicht ein Versuch für eine logische Erklärung des 'Wunders' gemacht, sondern penetrant die größte 'Rätselhaftigkeit' des 'Abbiegens-nach-oben' infolge der Wirkung der "Dunklen_Energie" gefeiert.
Belehrung: Im echten «Hubble-Diagramm» müsste der gemessene «HubbleParameter»-Verlauf beim ‘Überwiegen‘ der "Dunklen_Energie" sich „nach-oben“ wenden. Allerdings wurde dieses „Abbiegen-ach-oben“ nicht bei einem echt «Hubble-Diagramm», sondern beim schon vorher gemessenen irrigen »Hubble_plot« gemäß dem nachstehend gezeigten ‘btenSchaubild‘ gefunden, (woran die Kommentare von FilipeAbdalla für sich selbst sprechen.)
Im nachstehenden ‘bten-Schaubild‘ soll der Pfeil bei „Accelerating“ die „Wendung der Kurve nach-oben“ signalisieren.
.
Diese Wendung der Kurve „nach-oben“ soll zudem die beschleunigende Wirkung, und überhaupt, die daraus gefolgerte Existenz von "Dunkler_ Energie" erläutern.
Bei dem nun nächsten‘cten-Schaubild‘ handelt es sich im ein solches vom Typ echtes «Hubble-Diagramm», welches hier die markante Überschrift "..KosmoEntfernungsLeiter.." hat.
Diese Grafik hat einen besonders interessanten Bereich um die "ž-Werte=1,0" herum, dort wo sich die violette geschweifte Klammer für die NobelpreisMessErgenisse befindet.
Die Grafik zeigt insbesondere auf, dass ‘wir uns hier&heute‘ etwa in der SymmetrieMitte von ±35 [Dekaden mit abwechselnden Exponenten] befinden..
Diese SymmetrieMitte beim nachfolgenden ‘cten-Schaubild‘ stellt die ‘Relation‘ "pro z-Wert=1" oder für "100[GHz]" oder "für 3[mm] Wellenlänge" oder "pro 1[°K]" dar.
{Ich selbst trage mit mir ständig jenen Merksatz herum, den ich mir aus der Boltzmann'schen Konstante und dem Planck'schen Wirkungquantum zusammengereimt habe: „103,4[GHz] pro[°K]“ ist eine Naturgesetzlichkeit.}
Also, deswegen wird nachstehend für die Mitte der ["z-Werte"-Dekaden] „103,4[GHz] pro[°K] und pro[z-Wert=1,0]“ festgelegt.
Vorstehend: 'ctes-Schaubild' mit der –(jedoch hier noch mit missglückter SymmetrieMitte)–, die auch bildlich bei "ž=1,0" zu sein hat.
Hier zu dieser SymmetrieMitte zwei zugehörige Zeilen aus anderen URLs:.
Für 100GHz/3mmgilt"ž=10^0,014514"//"ž=1,0340.10^±0"gilt"θ=10^0.01,4484[°K]"//"9,672.10^–1[°K]";
Für 103,4GHz/2,9mmgilt"ž=10^0,0000333"//"ž=0,9999231"gilt"θ=10^0,0000334[°K]"//"1,000077[°K]".;
.
Dann müsste zu dem Bereich der SymmetrieMitte mit "ž=1,0", (nämlich davon "ž=1089-fach" entfernt), eine Lokalität gegeben haben, wo "ž=0-fach" gegolten hat.
Und, weil sich von dort aus die CMB-Erscheinung ausgebreitet hat, müsste –(logisch naheliegend)– die AbsendeLokalität für "ž={1/1089-fach}" bei "ž=0,9.10^–4-fach" gewesen sein.
Jetzt müsste ich wissen, wieviel "ž-[Dekaden]" hinab bzw. hinauf zum Absende-Ort der CMB-Erscheinung, (wo "380000[LJ] nach dem Urknall" der ϾInflationsϿ-Peak geendet hat, anzuberaumen seien.
In nachstehenden 'ytenSchaubild' ist die Mitte bei "ž=1,0" angesetzt.
Von der Mitte bei "ž=1,0" bis unten bei "ž=0" müssen "13,8[MrdLJ]" gerechnet werden. {Dafür ist die ermittelte Rotverschiebung "ž=1,0-fach"}.
Für die Strecke [ab AbsendeOrt des CMB-Signals bei "380000[LJ] nach dem Urknall" bis 'hier&heute' "13,8[MrdLJ] nach dem Urknall" möchte ich "13,7[MrdLJ] Laufzeit" schätzen.
Die geschätzte Differenz "0,1[MrdLJ] Laufzeit" gleich "0,0001[MioLJ] Laufzeit" ist mit der ermittelten Differenz für {"ž=0,9.10^–4" mal "13,8[MrdLJ] " = "1,242[MioLJ] Laufzeit"} zu vergleichen.
Wie man sieht, ist "0,0001[MioLJ] Laufzeit" ≠ "1,242[MioLJ] Laufzeit".
Das Kosmologische Standardmodell kann diesbezüglich nicht zu stimmen.
Im vorstehenden 'ytenSchaubild' müsste ich für diese vielen ž-[Dekaden]" –(aus SymmetrieGründen insgesamt zirka 2mal 35[Stück] vorsehen.
Und, für die ϾInflationϿ-Peak-Seite muss ich 1mal 35[Stück] "ž-[Dekaden mit negativen Exponenten] vorsehen. Aber, ich habe nur bis "ž={1/1089-fach}=0,9.10^–4-fach" gebucht. Wie obig ausgeführt ist, passen "z=1089-fach" und "380000[LJ] nach dem Urknall"überhauptnnicht zusammen.
Das Kosmologische Standardmodell kann diesbezüglich nicht zu stimmen.
(Ab hier gilt ein RückWechsel zum unterbrochenen Thema.)
In der weit oben gezeigten Tabelle[321]S342bisS345, (welche dort die Bezeichnung ‘atesSchaubild‘ hat), gibt es die [3.]Zeile mit der "(FranzEmbacher’schen) Rotverschiebungs-Entfernungs-Relation", wozu ich die nachfolgende FunktionsGrafik aus meiner ‘RaritätenSammlung‘ nachträglich vorzeigen möchte.
Diese Grafik heißt hier nachstehend ‘xtes-Schaubild‘.
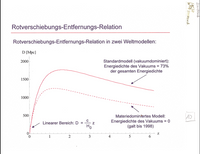
Nachstehendes –(wegen seines RaritätenWertes nachgeholtes)– ‘xtes-Schaubild‘ zeigt die "Rotverschiebungs-Entfernungs-Relation".
Diese "Rotverschiebungs-Entfernungs-Relation" hatte ich im Inhaltsverzeichnis der hochinteressanten Homepage-Seite von "Franz Embacher Homepage - univie.ac.at" gesucht, jedoch lange nicht wiederfinden können.
Und, deswegen hatte ich zuerst angenommen, dass die seltsame ‘Buckelkurven‘- Funktionalität –(im Zuge neuerer Erkenntnisse)– in die Kritik zum Standardmodell geratenen sei und deswegen verworfen worden sei.
Hinweis: Die nachstehende (im doppelt-linearen KoordinatenSystem "häßliche") 'Buckelkurve' wäre/ist im doppelt-logarithmischen KoordinatenSystem eine "schöne" 'Höckerkurve', weil die Höckerkurve' zu ""ž=1" symmetrisch ist.
Ich ging schon davon aus, dass diese Folie[10] wegen Mängel am Kosmologischen Standardmodell zurückgezogen worden sei (und nun für 'ewig' aus den offiziellen Unterlagen 'verschwunden' sei).
Aber, als ich in den nebensächlichen Verzeichnissen nochmals gezielt nach der „Rotverschiebungs-Entfernungs-Relation“ recherchierte, stieß ich auf eine noch existierenden "PowerPoint Presentation-univie.ac.at", worin diese Folie noch enthalten ist.
Für mich war/ist interessant, dass das Maximum der BuckelKurve bei "ž=1,64" für die Entfernung "D=1777[Mpc]" bzw. für den Zeitpunkt "t=5,8[MrdLJ]" liegt.
Aber, diese ‘Rarität‘=Folie[10] =‘xtenSchaubild‘ als Funktionsdiagramm gesehen noch spannender; den die Funktionalität ist falsch-herum gepolt!
Als Funktionalität der Grafik wird nämlich –(wie aus der lesbaren Kommentierung „linearer Bereich "D=(c/H0).z" zu entnehmen ist)– richtigerweise ein »Hubble_plot« angenommen, der aber hat bekanntlich eine {y/x}-KoordinatenVerkehrung!
.
Hier SzenenWechsel:
Beim weiter unten stehenden ‘dten-Schaubild‘ mit der Überschrift "Abschätzung der Energetigkeit bei "ž=200", werden zwei hoch-interessante chronologisch versetzte Dateien als zwei MesswertCluster dargestellt, und zwar
…links unten von der Oklahoma Group sowie
… in der Mitte von der California Group.
.
Hinweis: Das MesswertCluster von der Oklahoma Group ist gleich richtig-herum orientiert im echten «Hubble-Diagramm» dargeboten gewesen.
Jedoch das spätere MesswertCluster von der Califorrnia Group, welches in der Mitte des ‘dten-Schaubild‘ dargeboten wird, war vor meiner Spiegelung vorher als »Hubble_plot«-Schaubild‘ angeliefert worden und musste daher erst um die 45°-Winkelhalbierende „gespiegelt“ werden, damit es –(in der notwendigerweise echten «Hubble-Diagramm»-Funktion)– in die Grafik eingebunden werden konnte.
.
Somit ist mit der Spiegelung beim ‘dtenSchaubild‘ m.E. endgültig geklärt worden, dass ein vorheriges RobertKirshner’isches „modern Hubble_diagram“ kein echtes "Hubble-Diagramm" war, und, dass deswegen die fatale Koordinaten-Verkehrung entstanden ist.
Aber das vorher irrige »Hubble_plot«-Schaubild war trotzdem nicht ‘unnütz‘, sondern sogar für die Verleihung des Nobelpreises m.E. von unermesslich großen Wert, weil ja wie es das Messwerte-Cluster in der Mitte eindeutig aufzeigt, dass die «HubbleParameter»-Kurve „abzuklingen beginnt“.
Nachstehend folgt 'dtes-Schaubild'.
Vorstehend 'dtes-Schaubild'
Hierzu weiter-denkend hatte ich ja, wie ersichtlich, im
‘dten-Schaubild‘ den Versuch gewagt, für die CMB-Rotverschiebung "ž=1089-fach" eine spekulative „Abklingung von "ž=1089-fach" auf "ž=200-fach"“ anzunehmen und weiter-zugehörig eine extremspekulative Extrapolation aufzuzeichnen.
Dieser aufgezeichnete extrem spekulative Hubble-Parameter»-Verlauf, welcher im ‘dtenSchaubild‘ mit der schwarz-gestrichelten Kurve gezeigt worden ist, sowie schon in dem anderen ‘ctenSchaubild‘ ab der violetten geschweiften Klammer extrapolierend gemeint war, ergab, dass dieser Verlauf im nachstehenden ‘etenSchaubild‘ m.E. recht gut zu dem „k-ê-för-migen sättigungsbegrenzten“ violettfarbenen Verlauf passen würde.
Diese k-ê-Sättigungs-Kurve würde nach 3 Stück Hubble-Zeitkonstanten je "To=13,8[MrdLJ]" 95% des 100%-Endwertes angenommen haben.
Und, dieser Kurvenverlauf der «HubbleParameter»-Kurve würde ja für das Urknall-Modell anzunehmen sein.
.
Für das andere Urprall-Modell würde hingegen, –(ebenfalls in dem vorstehenden ‘etenSchaubild‘)– der orangene Verlauf der ‘endenden‘ –cos-Kurve bzw. der –(ab der SymmetrieMitte beginnende Verlauf der +sinus-Kurve)– gelten.
.
Für beide Klassik-Modelle würde die ‘gewagte‘ Extrapolation "ž=1089-fach" gelten. Jedoch die Logik m.E. besser für den orange beginnenden Verlauf der +sinus-Kurve passen.
.
Für beide Klassik-Modelle gilt:
Der KurvenBeginn ist unterhalb der Symmetrie-Mitte 35 [Dekaden mit negativen Exponenten] zu denken, welchen Bereich ich ja neuerdings zur ϾInflationsϿPhase zugehörig rechne.
.
Erinnerung: Das „neuerdings“ steht bei mir für die Ablösung von meiner bisherig-totalablehnenden Haltung, nämlich dass die ϾInflationsPeakϿPhase gedanklich völlig abgetrennt von der ϿExpansions-BlähϾPhase einzuklassieren sei.
.
Dieses ging damals auf meinen entschiedenen Widerspruch zu einer Aussage von GüntherHasinger zurück, nämlich: „Die ‘Inflation‘ wirke heute noch innerhalb der ‘Expansion‘ fort“.
Anmerkung: {Und, spätestens hier muss ich auch die strenge Klärung herbeiführen, welche Anführungszeichen ich
…bei der ‘Inflation‘ bzw.
... bei der ‘Expansion‘ zu setzen habe.
.
Nach der logischen Zugehörigkeit der ϿEntropieϾ, die ja zur ϿExpansionϾ dazugehört, gilt dann die Zugehörigkeit der ϾInflationϿ zur ϾSymtropieϿ.
Diese k-ê-Sättigungs-Kurve würde nach 3 Stück Hubble-Zeitkonstanten je "To=13,8[MrdLJ]" 95% des 100%-Endwertes angenommen haben.
Und, dieser Kurvenverlauf der «HubbleParameter»-Kurve würde ja für das Urknall-Modell anzunehmen sein.
Für das andere Urprall-Modell würde hingegen, –(ebenfalls in dem vorstehenden ‘etenSchaubild‘)– der orangene Verlauf der ‘endenden‘ –cos-Kurve bzw. der –(ab der SymmetrieMitte beginnende Verlauf der +sinus-Kurve)– gelten.
.
Für beide Klassik-Modelle würde die ‘gewagte‘ Extrapolation "ž=1089-fach" gelten. Jedoch die Logik m.E. besser für den orange beginnenden Verlauf der +sinus-Kurve passen.
.
Für beide Klassik-Modelle gilt:
Der KurvenBeginn ist unterhalb der Symmetrie-Mitte 35 [Dekaden mit negativen Exponenten] zu denken, welchen Bereich ich ja neuerdings zur ϾInflationsϿPhase zugehörig rechne.
Erinnerung: Das „neuerdings“ steht bei mir für die Ablösung von meiner bisherig-totalablehnenden Haltung, nämlich dass die ϾInflationsPeakϿPhase gedanklich völlig abgetrennt von der ϿExpansions-BlähϾPhase einzuklassieren sei.
.
Dieses ging damals auf meinen entschiedenen Widerspruch zu einer Aussage von GüntherHasinger zurück, nämlich: „Die ‘Inflation‘ wirke heute noch innerhalb der ‘Expansion‘ fort“.
Anmerkung: {Und, spätestens hier muss ich auch die strenge Klärung herbeiführen, welche Anführungszeichen ich
…bei der ‘Inflation‘ bzw.
... bei der ‘Expansion‘ zu setzen habe.
.
Nach der logischen Zugehörigkeit der ϿEntropieϾ, die ja zur ϿExpansionϾ dazugehört, gilt dann die Zugehörigkeit der ϾInflationϿ zur ϾSymtropieϿ.
Nachstehend: 'etes-Schaubild'.
Vorstehend: 'etes-Schaubild'
Erwartung: (bezüglich 'Energetigkeit' gemeint):
Zumeist werde ich –(bei der ja größer werdenden ϿExpansionϾ mit größer werdender ϿEntropieϾ)– zu tun haben.
Jedoch muss ich bedenken, dass bezüglich der ρDichte dabei eine Verdünnung eintritt.
Also muss ich so denken, dass ich beim sozusagen „Zerfall des Universums“ mit dem Boyle Mariotte’schen P.V=Ŗ.T-Gesetzes zu rechnen haben werde.
Wiederholng:. Beim Urknall-Typ zählen die "ž-Werte" bereits ab ganz unten, wo die ϾInflationsϿPhase beginnt, bei den 35 [Dekaden mit negativen Exponenten] ab dem Anfang der ErsatzGerade, welche das Entfernungsmodul darstellt.
Allerdings biegt «HubbleParameter»Kurve von der ErsatzGerade ab.
Die "ž-Werte" zählen also neuerdings für die Nachwehen der ϾInflationϿ in der Grafik von ganz unten bis hinauf zu der SymmetrieMitte 35 [Dekaden mit negativen Exponenten], welche Symmetrie-Mitte ja bei "z=10^±^0=1,0" angesiedelt ist.
.
Beim Urprall-Typ zählen die "ž-Werte" ebenfalls ab ganz unten, wo die ϾInflationsϿPhase beginnt und nach dem „Urprall“Durchgang entlang der [–cos-Kurve], (welche hier ja genau die «HubbleParameter»Kurve repräsentiert), und wo neuerdings 35 [Dekaden mit negativen Exponenten] von ganz unten bis hinauf zu der SymmetrieMitte gedacht werden müssen, welche SymmetrieMitte bei "z=10^±^0 =1,0" angesiedelt ist.
.
Bei den Klassik-Modellen beginnen beide mal die Hubble-Parameter-Verläufe im echten «Hubble-Diagramm» gedacht ‘ganz unten‘ bei "ž=10^–35".
Und, der Verlauf der «HubbleParameter»Kurve folgt zunächst der EntfernungsmodulErsatzGerade etwa bis zur Symmetrie-Mitte bekanntlich bei "z=10^±^0 =1,0" angesiedelt ist.
.
Da dieser Messbereich vorstehend bei der ‘dritten‘ Grafik schlecht zu erkennen ist, hatte ich schon eingangs bei dem ‘ctenSchaubild‘ auf die geschweifte violette Klammer hingewiesen.
.
In der ‘dritten‘ Grafik werden
_ beim Urknall-Modell entlang einer k-ê-SättigungsKurve, die nach 3 Stück H0-Zeitkonstanten typischerweise 95% des Maximalwertes erreicht.
Oder,
_ beim Urprall-Modell folgt die «HubbleParameter»-Kurve der auslaufenden der [–cos-Kurve], (welche ja auch hier
genau die «HubbleParameter»Kurve repräsentiert) und zu der neuerdings 35 [Dekaden mit negativen Exponenten] ab der Symmetrie-Mitte bis ganz oben hinauf zum Maximum bei "ž=10^+35=cos_360°" gedacht werden müssen, welche SymmetrieMitte bekanntlich bei "z=10^±^0 =1,0" angesiedelt ist.
.
Die Steigung der «HubbleParameter»Kurve bei der Symmetrie-Mitte zu "tan_α=45°" für den ‘m‘Wert =1,0 entspricht zugleich der «Hubble-Konstante» "H0=72[km/s] pro [Mpc]" und der ‘klassisch‘-bewerte-ten Rotverschiebung ž=1,0" im echten «Hubble--Diagramm» beim UrprallModell.
.
Aber, beim Urknall-Modell wird der Skalenfaktor "ą" ab dem Urknall gezählt und hat bei der «Hubble’schen Zeitkonstante», die "To=13,8[MrdLJ]" beträgt, den dimensionslosen Wert "ą=1,0".
Für die Größe des Universums wird, beim Ur-knallModell so getan, als ob sie keiner Sättigungs-Begrenzung unterliegen würde, so_dass nach "To=13,8[MrdLJ]" die ‘hier&heutige‘ Größe "ą=1,0" erreicht worden sei.
Jedoch muss beim Urknall-Modell für die Entwicklung der Größe mit der k-ê-StättigungsFunktion kalkuliert werden, die im echten «Hubble-Diagramm» ein ‘Abklingen‘ der «HubbleParameter»Kurve bewirkt.
Typischerweise bewirkt k-ê-StättigungsFunktion, dass nach 3’Stück‘ "13,8[MrdLJ]"-ZeitKonstanten, also nach "42[MrdLJ]" 95% der schließlichen 100%-Größe von zirka "46[MrdLJ]" erreicht würden.
..
Somit bin ich bei den "46[MrdLJ]", die das Λ-CDM-Modell als ‘PartikelGrenze‘ anerkennt.
Das nun zu diskutierende Λ-CDM-Modell geht ebenfalls von einem Urknall aus. Und es wird so getan, als ob die Vergrößerung keiner Sättigungs-Begrenzung unterliegen würde, so_dass nach "To=13,8[MrdLJ]" die ‘hier&heutige‘ Größe "ą=1,0" erreicht worden sei.
Die von mir so benannte «Hubble’sche Zeitkonstante» heißt aber hier für’s Weltalter "To=13,8[MrdLJ]" und die Größe des Universums hat den quantitativen dimensionslosen Wert "ą=1,0".
.
Wichtige Einzelheit beim Kosmologischen Standardmodell:
Die Rotverschiebung wird beim Λ-CDM-Modell in gegenläufigen "z-Werten" zu den "ą-Werten "zugeordnet, weil offenbar angenommen wird, dass hohe Strahlungs-TemperaturWerte hohe ϿEntropieϾ ausmachen müsse.
{Allerdings ist das Stichwort ‘Entropie‘ nicht in Lit.[321] sowie auch sogar im SpringerBuch-Hauptwerk Lit.[994] nicht zu finden!}.
Dem Urprall-Modell zugehörig ist//zugehörig wäre, falls am Beginn des Universums ein „Urknall“ zu bedenken wäre.
Auch bei den "ž-Werten" in der untergeschossigen Reihe der [1.]Zeile der Tab.[321]S342bisS345 ist zunächst ein Urknall“ zu bedenken.
Die "z-Werte" in mittigen Reihe der [1.]Zeile der Tab.[321]-S342bisS345 sind original für’s Λ-CDM-Modell gültig, und man erkennt, dass für den lokal-momentan gedachten Fall "z=1/(ž+0)" beide Modelle gleichwertig wären.
Jedoch wird in der derzeit praktizieren HochschulLehre noch das m.E. irrige „Kosmologische StandardModell“ also das gängige Λ-CDM-Modell gefeiert.
Weil nach Lit.[321]S397 im Λ-CDM-Modell die Formel für‘s vorgegebene "Re/R0"-Verhältnis gilt und sofern {"Re"=‘nahe dem Urknall‘} bzw. sofern {"R0"=‘hier&heute‘} bedeuten, würde, kämen
_ in den laufenden [x,ten]Spalte der Tab.[321]S342bisS345 für
_ die laufenden "Re/R0-Verhältnisse" bzw. anstelle der
_ die laufenden schwarzen "z-Werte" die versetz&
_verkehrten roten "ž-Werte" heraus:
[21,0]"Re/R0=10^35" "z=10^35">"z=1/(1+10^35)"< "ž=10−^35"
[20,5]"Re/R0=10^5" "z=10^5" =>"z=1/(1+10^5)"<= "ž=10^−5"
[20,0]"Re/R0=1090" "z=1089"=>"z=1/(1+1089)"<"ž=0,0009"
[19,9]"Re/R0=1001" "z1000"=>"z=1/(1+1000)"<"ž=0,0009"
[19,3]"Re/R0=101" "z=100"=>"z=1/(1+100)"<="ž=0,009"
[16,5]"Re/R0=11" "z=10"=>"z=1/(1+10)"<="z=0,091"
[15,9]"Re/R0=10" "z=9"=>"z=1/(1+9)"<="ž=0,1"
[12,5]"Re/R0=6" "z=5"=>"z=1/(1+5)"<="ž=0,17"
[8,00]"Re/R0=3" "z=3"=>"z=1/(1+2)"<="ž=0,33"
[7,00]"Re/R0=2" "z=2" =>"z=1/(1+1)"<="ž=0,5"
[6,00]"Re/R0=1,7" "z=1,7">"z=1/(1+0,7)"<"ž=0,59"
[3,00]"Re/R0=1,5" "z=0,5"=>"z=1/(1+0,5)"<"z=0,67"
------------------------------------------------------------------------------------------------------------
[4,00]"Re/R0=1" "z=1" => "z=1/(1+0)" <= "ž=1"
-------------------------------------------------------------------------------------------------------------
[1,99]"Re/R0=1,1" "z=0,1"=>"z=1/(1+0,1)"<="ž=0,91"
[1,01]"Re/R0=1,01" "z=0,01"=>"z=1/(1+0,01)"=>"ž=0,99"
[1,00]"Re/R0=1,001" "z=0,001">"z=1/(1+0,001)">"ž=0,999"
In der hellblau hinterlegten Spalte mit den schwarzen
"z-Werten" herrscht das derzeit “gültige „Kosmologische Standard-Modell“
Und darin gilt jener Sachverhalt, dass die CMB-Emission in nächster, nämlich in "z=0,001" Nähe zum Urknall abgesandt worden sei; und, dass dafür, (effektiv mit "10^+35-facher" Rotverschiebung ‘auf der Erde‘ angekommen), ein "z-Wert =10^±0", also "z-Wert=1,0" gemessen worden sei.
Dieses heißt dann, dass schematisch im Λ-CDM-Modell, also in der Tab.[321]S342bisS345 folglich weiter gilt, dass in der [9.]Zeile jeweils höchste "z-Werte" jeweilig höchste [°K]-Strahlungs-TemperaturWerte bedeuten sollen.
Oder, es bedeutet, dass für die mittleren "z-Werte" auch mittlere [°K]TemperaturWerte (um "300[°K]" herum) gemein sein müssten.
Bzw. es bedeutet, dass niedrigst-gemessene "z-Werte" (um "z=0,0001" herum) auch niedrigste Weltraum-TemperaturWerte (um "3[°K]" herum) haben müssten.
.
Daraus folgt wiederum formal, dass eine gemessene Rotverschiebung von "ž=10^−4" sowie die zugehörig gemeinte Abkühlung auf niedrigste Temperatur für ‘hier&eute’ (auf der Erde, um "T=3[°K]" herum) zwar nicht den totalen KälteTod bedeuten müsste, sondern dass dabei an eine Abkühlung (auf "1[°K]" oder unter "0,1[°K]") gar_nicht gedacht worden ist.
Dabei würde die Abkühlung auf ultimativ-positiven "ž=10−^35"
zulässig zu denken gewesen, weil erst darunter der Erstarrungstod allen Lebens zu erwarten ist.
Derweil ja im Λ-CDM-Modell offenbar jene im Grenzfall messbare Rotverschiebung die „auf das LaborSystem ‘hier&eute auf der Erde‘ rückbezogen“ gemeint ist, bei "ž=10−^35" noch nicht zu Ende wäre, (nämlich, weil ja die Tabelle erst bei "z=0" aufhöre, kann nicht die „Hubble’isch genormte Verfügung "z= "pro [Mpc]“ gemeint sein; und deswegen schon alleine muss das Λ-CDM-Modell falsch sein musss.
Fortgesetzter Vergleich; sozusagen [nicht-versetzt-verkehrt] betrachtete Wiederholung vorstehender Tabelle. In der [21,0]ten Kolonne ist die [Spallte in der Tab.[321]] aufgeführt.
Die grüne "Re/R0"Kolonne gilt allgemein, das heißt für beide Modelle, das Λ-CDM-Modell und das klassische Urknall-Modell. Die "z=10^35"Kolonne gilt das Λ-CDM-Modell, also für das „irrige“ Kosmologische Standardmodell. Der Raum dazwischen enthält die Umrechnungen.
Die roten "ž-Werte" gelten für „physikalisch richtige“ klassische Urknall-Modell.
--------------------------------------------------------------------------
[21,0]"Re/R0=10^35" "z=10^35">"z=1/(1+10^35)"< "ž=10−^35"
[20,5]"Re/R0=10^5" "z=10^5" =>"z=1/(1+10^5)"<= "ž=10^−5"
[20,0]"Re/R0=1090" "z=1089"=>"z=1/(1+1089)"<"ž =0,0009"
[19,9]"Re/R0=1001" "z1000"=>"z=1/(1+1000)"<"ž=0,0009"
[19,3]"Re/R0=101" "z=100"=>"z=1/(1+100)"<="ž=0,009"
[16,5]"Re/R0=11" "z=10"=>"z=1/(1+10)"<="z=0,091"
[15,9]"Re/R0=10" "z=9"=>"z=1/(1+9)"<="ž=0,1"
[12,5]"Re/R0=6" "z=5"=>"z=1/(1+5)"<="ž=0,17"
[8,00]"Re/R0=3" "z=3"=>"z=1/(1+2)"<="ž=0,33"
[7,00]"Re/R0=2" "z=2" =>"z=1/(1+1)"<="ž=0,5"
[6,00]"Re/R0=1,7" "z=1,7">"z=1/(1+0,7)"<"ž=0,59"
[3,00]"Re/R0=1,5" "z=0,5"=>"z=1/(1+0,5)"<"z=0,67"
------------------------------------------------------------------------------------------------------------
[4,00]"Re/R0=1" "z=1" => "z=1/(1+0)" <= "ž=1"
-------------------------------------------------------------------------------------------------------------
[1,99]"Re/R0=1,1" "z=0,1"=>"z=1/(1+0,1)"<="ž=0,91"
[1,01]"Re/R0=1,01" "z=0,01"=>"z=1/(1+0,01)"=>"ž=0,99"
[1,00]"Re/R0=1,001" "z=0,001">"z=1/(1+0,001)">"ž=0,999"
Re/R0=10^5"R
In der gelb hinterlegten Zeile mit den roten "ž-Werten" herrscht das eigentlich schon immer physikalisch gültige Klassik-Modell.
Und, darin gilt jener Sachverhalt, dass die CMB-Emission aus nächster, nämlich aus " ž=0,999-facher" nächster Nähe zum Urknall abgesandt worden sei; und, dass dafür für den 'NormAbstand "1[Mpc]" eine Rotverschiebung von "ž=11089-fach" ermittelt worden sei.
Der andere gedachte Normalfall dass eine Rotverschie-bung von über "ž=1,0", vielleicht für Quasare mit exotischen "z-Werten" von maximal "z=33" ermittelt worden ist, kann nun „klassisch“ erklärt werden.
Ein von sogar "ž=10^+32-fach" ist zwar messtechnisch nicht vorgesehen; aber im Sinne primordialer Nukleo-synthese gedanklich akzeptabel für hohe »Entropie«.
Denn, gemäß den BoyleMariotte&Boltzmann’schen Gesetzen könnte hohe »Entropie« (im Sinne eines ‘hoch-turbulenten Wirrwars‘ der GasMoleküle) mit hoher Tem-peratur verknüpft gedacht werden. Dieses scheint bei den mittelgeschossigen schwarzen z-Werten, die in der [1.]Zeile der Tab.[321]S432-bisS345 von links nach rechts ansteigend sind, gemeint gewesen zu sein.
Aber, hohe »Entropie« bedeutet hohe „Zerbrochenheit“, nämlich in viele Boltzmann‘sche Phasen.
Und, hohe »Entropie« kann erst am Ende der Reihe stehen, weil mit niedrigster »Entropie« begonnen wird. Das heißt, die niedrigsten "z-Werte" beginnen mit "ž=10−^35" bei höchster Temperatur "T=10^+32[°K]" um dann mit Beginn mit niedrigster, nach-folgend ansteigender »Entropie« und synchron ansteigenden "ž-Werten" bedeutet, welche "ž-Werte" in der untergeschossigen Reihe der [1.]Zeile von rechts nach links ansteigend oder (zur Kontrolle ) von links nach rechts fallend stehen müssen.
Von rechts nach links ansteigende "ž-Werte" geht nur von ‘klein‘ = "ž=10−^35" nach ‘groß‘ = "ž=10+^35" hin.
Das heißt, die »Entropie« kann nur [von niedrig bei hoher Temperatur] auf [hoch bei niedriger Temperatur] ansteigen.
Sonderzeichen1-------------ᴰᴺᴹɆÐ
⅛⅜⅝⅞¼½¾⅓⅔ √∞ " ^ ~ ≈‹›«» ′ ‚‛ „“ – ∝≙≚≗≛≅≜ ≤ ≥ ≠ ≡ ⌂ ±
αβγδεηθικλμνξοπρςστυφχψω ΑΒΓΔΕΖΗΘΙΚΛΜΝΞΟΠΡΣΤΥΦΧΨΩ ąáàãäæăâąã@ÅĄ þÞ čĉćċ¢₡©Ↄ ₫∂ϑΔÐᴰ ēėêéęĘÉĒɆ€℮ ƒᶂφɸ ĝġĜĠĞ ĥħĤĦ ὶîijį ĸœ₭ ℓ₤ ᴹжЖ ñňᴺ ṄŇÑ Øøόõôѳọ Ω₀ ₱ № υϋύὺῠ řŗŖŘ® ŝśšϭϬ τŤţť₮ ∩ẈẄẆ žʒ ĸ-ê {Ē\/Þ²}- (υ²=[2·Ğ·M/Ř]) "m/mѳ = 1/√[1– (υ/c)²]" ƒ(Řx) ‼Řx‼ ^•‽ ⁽⁾₍₎